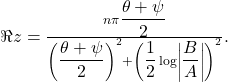Category: I Can has Maths?

Testing LaTeX

Liek whoa! Two posts in one day!

\LaTeX, in case you didn’t know, is a very sweet markup language for making professional-looking documents and is used pretty heavily in the Maths and Sciences, because it has wicked formula support. If you’ve seen math formulas on Wikipedia, then those were created with LaTeX. I’ve recently discovered that there’s a pretty sweet WordPress plugin, Easy LaTeX that allows you to embed formulas on your blag.

Though, I probably won’t use it very often (read: possibly never again after this post), I thought that I’d at least show it off once. I might even update my infamous “Derivatives Made Easy” (the #1 result on google for that phrase… I still get a lot of hits to it) post with nice-looking formulas instead of the paint-drawn ones I have now.

So, here’s some of the neat-looking stuff you can make with LaTeX:

\Re{z} =\frac{n\pi \dfrac{\theta +\psi}{2}}{ \left(\dfrac{\theta +\psi}{2}\right)^2 + \left( \dfrac{1}{2} \log \left\lvert\dfrac{B}{A}\right\rvert\right)^2}.

Math Time! Derivatives Made Easy!

So, there I was during IRC, just chatting along, when someone asked some random calculus question, I got it right, and then they asked me to explain how to do derivatives the “easy” way. I was originally going to do this through MSN Messenger with the nifty little drawing conversation feature, but alas, the person in question didn’t support Handwriting. Instead, I’m now going to make a short little blog post about how one can easily do a derivative. This is just the easy stuff, remember, I’m not getting into derivatives of fractional functions or something like that.

Another thing, these graphical examples were done quickly in paint, so don’t make fun of me ;_;

First, we have a simple function f(x) = x^2 – 3x – 4, as displayed in the picture below:

For simple derivatives such as these, we first have to remember some properties of exponents, such as: any variable by itself (or with a coefficient) is variable^1 . If a coefficient is by itself, we can say that it the coefficient multiplied times the variable to the zeroeth power — variable^0 . We can use these properties to modify our original equation to look something like this:

Now that we have the modifications out of the way, we can get to the actual derivation. For equations like these, to get the derivative, you multiply the power by the coefficient, and then subtract one from the power, as shown in the drawing:

Then, you use a bit of simplification, and you’ll come out with f‘(x) = 2x – 2, as shown below:

See? It’s not really that hard. :)